Hablando de electricidad: Corriente Continua
Hola a todos. Últimamente he querido hacer varios post centrándome en la actualidad tecnológica y en aparatos o máquinas concretas. Aquí y ahora vamos a hablar de electricidad, comenzando con una introducción de conceptos básicos necesarios y siguiendo con un conjunto de ideas interesantes y extensas acerca de... La corriente continua.
NOTA: En este tipo de enseñanza básica no profundizaré acerca de métodos sistemáticos o complejos para la resolución de circuitos (como métodos de malla y nodos) a no ser, claro está, que sea estrictamente necesario.
CONCEPTOS BÁSICOS
Pongamos sobre la mesa diferentes definiciones necesarias para poder entender mejor el tema. En un circuito eléctrico tenemos tres elementos clave: Una fuente de generación, una carga y un medio de transmisión de energía (los cables). Para entenderlo mejor veamos un caso análogo con un circuito hidráulico: La bomba (fuente generadora) impulsaría el fluido (Intensidad de corriente) que acabaría generando un empuje en un elemento que lo necesite (Carga):
El generador puede ser una fuente de tensión (como el de la figura), de manera que entre sus extremos impone una diferencia de potencial o tensión. Se denomina diferencia de potencial o tensión a la energía necesaria para transportar una carga de un punto a otro. O en forma de ecuación sería dV=dW/dq. Donde V es voltaje o tensión (medida en voltios (V)), W es trabajo o energía (medida en julios (J)) y q es carga (medida en Culombios (C)). Como vemos estoy trabajando con ecuaciones diferenciales así que para los que no tengan una buena base matemática esto equivale a la expresión común V=W/q (al fin y al cabo un diferencial no es más que un trozo o elemento de un total, por ejemplo dV no es más que una porción de V, estos son, conceptos de integración y ecuaciones diferenciales en los cuales no haré mucho hincapié pero es debido mencionarlo).
Como ya sabemos en un circuito eléctrico cerrado con esta configuración existe un flujo de electrones que va del punto + de la pila al -. Ya he dicho que la fuente de tensión impone una energía a las cargas, de manera que los electrones no fluyen en esta dirección, sino que su recorrido natural es del polo negativo (-) al positivo (+). Posteriormente los electrones se ven desplazados y circulan por el cable conductor. Al ser de este material la oposición que hace al flujo es más baja que si fuera otro con mayor resistencia, por lo que consiguen moverse con más facilidad.
Ahora llegan a un elemento conocido como carga. Se define carga como un elemento del circuito que consume potencia y en el cual la tensión cae. Las resistencias en electricidad son cargas. Para ser alimentadas por ellas debe circular una intensidad de corriente. Se define intensidad de corriente como la cantidad de carga que fluye en un determinado instante, o sea I=q/t, o lo que es más preciso I=dq/dt, donde I es intensidad de corriente (medida en amperios (A)). Por lo tanto, cuanta mas carga fluya en un tiempo reducido la intensidad será mayor.
Ahora bien, para que un elemento del circuito sea carga la intensidad de corriente debe entrar por si polo positivo (+). ¿Entonces si por una fuente entra la intensidad por el + es una carga?
La respuesta es si y no. Se puede comportar de ambas maneras. Las baterías recargables son un ejemplo de ello. Cuando las usamos para hacer funcionar nuestra cámara o móvil actúan como generadores. Por otra parte si las enchufamos para cargarlas actuarán como cargas.

Batería recargable para un móvil
NOTA: De la misma manera para que una batería genere tensión es necesario que la intensidad que pasa por ella entre por el polo - y salga por el +.
También existen fuentes de corriente, las cuales se basan en los mismos principios que las de tensión, solo que imponen la intensidad. Es decir, que si hay una fuente de corriente de valor 2 amperios por ese cable al que está conectada circularán 2 A independientemente de lo que haya conectado.
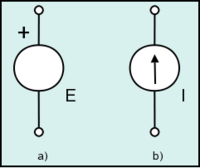
A la izquierda se ve una fuente de tensión, mientras que la de la derecha es de corriente.
Como nota de interés decir que si queremos saber si una batería está descargada (por ejemplo de un coche de 12 V) no bastaría medir la tensión de sus extremos con un voltímetro como pensarán muchos. Y es que aunque esté descargada el aparato seguirá midiendo 12 V. La razón es simple: Cada placa de la batería estará descargada en la misma proporción que la otra, de manera que la diferencia entre los extremos será igual, pero no será igual la tensión aplicada en uno de ellos.
Ya dicho todo lo anterior es hora de hablar de una de las leyes más importantes de la electricidad: La ley de Ohm
LEY DE OHM
La ley de Ohm nos dice que si tenemos un elemento con una resistencia R que es alimentado por una corriente de intensidad I, entonces aparece en sus extremos una tensión V. Se puede expresar de la siguiente manera:
V(R)=I*R
Parece muy sencilla, pero realmente merece una digna atención, pues se pueden extraer conclusiones muy interesantes de ella. Y es que en una resistencia del circuito tenemos los dos valores restantes que varían. Si en ella hay aplicada una tensión V muy pequeña, la intensidad también será pequeña, mientras que si V es grande, I también lo será. Por lo que mucha gente podría pensar que si yo aumento la tensión siempre la intensidad se verá incrementada. Esto no es cierto si consideramos que la resistencia total del circuito puede cambiar, por ejemplo conectando otra R. Para verlo mejor expliquemos primero otras dos leyes muy importantes: Las leyes de kirchoff.
1RA LEY DE KIRCHOFF
Esta ley me dice que en un circuito cerrado las intensidades entrantes en un nodo (punto donde confluyen mas de 2 caminos o ramas) deben ser igual a las salientes. Es decir: I1+I2+I3+...+In=0. Debemos de tener en cuenta los signos: Las entrantes PUEDEN ser positivas, así que las salientes serán de signo opuesto.
O dicho de una forma vulgar: "Las gallinas que entran por las que salen"
2DA LEY DE KIRCHOFF
Esta ley de habla sobre la tensión repartida en un circuito cerrado. La suma de tensiones en todo el sistema debe ser 0. Es decir V1+V2+V3+...+Vn=0. De la misma manera que en la 1ra, las tensiones generadas las PODEMOS considerar de signo positivo, mientras que las caídas de signo opuesto. Usando el circuito simple de la Ley de Ohm vemos que la tensión V generada por la fuente debe ser igual a la caída de tensión en la resistencia, por lo que se demuestra que en este caso que V=V (R) por lo que V(fuente)=I*R.
Ahora podemos explicar que ocurriría si ponemos otra resistencia en el circuito. 
Como vemos R es la anterior, mientras que ahora conectamos otra R de valor R´. Si aplicamos la 2da ley de kirchoff la tensión generada por la fuente debe ser igual a la suma de las que caen en R y R´ (V=VR+VR´). Si aplicamos la ley de ohm en esta ecuación nos queda que V=I´*R+I´*R´, ya que la intensidad es la misma en ambas resistencias.
Si ahora sacamos factor común vemos que V=I´*(R+R´). Esto quiere decir que en dos resistencias en serie yo puedo sumarlas para obtener otra resistencia nueva que sería la equivalente (Req). También se observa que la tensión que cae en la R no es V como antes, sino que es VR=I´*R. Es decir que la tensión de la fuente se ha repartido entre dos resistencias. Este tipo de circuito se conoce como Divisor de tensión. Además se ve que la intensidad que circula ahora no es I como antes, sino que ha cambiado, es I´, cuyo valor ha disminuido (con despejar I´ de la 3ra ecuación de la foto se ve mejor).
Pero ahora vamos a cambiar la configuración y conectemos la resistencia R´ en paralelo y cambiemos la fuente de tensión por una de corriente:
Vemos que ambas resistencias están conectadas entre los mismos puntos A y B. Esto quiere decir que la caída de tensión en ellas será la misma. Cosa que cambia con la intensidad, puesto que se reparte entre las dos ramas o caminos.
Si aplicamos la 1ra ley de Kirchof en el nodo A tenemos que I´=IR+IR´. Aplicando la ley de Ohm se ve que IR=V/R y de forma análoga IR´=V/R´. Entonces I´=((V/R)+(V/R´)).
Sacando factor común I´=V*((1/R)+(1/R´)). Resolviendo esta operación de suma de inversas y pasandolo al otro lado dividiendo se obtiene que I´*((R*R´)/(R+R´))=V.
De aquí deducimos que dos resistencias estarán en paralelo cuando la caída de tensión en ambas sea la misma (es decir que tengan puntos comunes A y B), y se pueden asociar en una resistencia equivalente Req, cuyo valor es Req=(R*R´)/(R+R´). Este modelo de circuito es equivalente al anterior y se denomina Divisor de corriente.
De aquí podemos sacar una conclusión de gran interés. Y es que la caída de tensión entre los puntos A y B antes de estar R´ NO es la misma que después. Como dijimos las fuentes de intensidad imponen la corriente, de manera que al conectar mas resistencias en paralelo ese amperaje se divide entre ellas, disminuyendo la caída de tensión entre los puntos citados.
Hasta ahora hemos hablado de fuentes que imponían tensión o intensidad, independientemente de lo que haya conectado. Os he mentido. En la realidad esto no es así, pero será mucho más fácil entenderlo si se ha comprendido lo anterior. Y es que la tensión que suministra una pila por ejemplo cambia en función de lo que se ponga en sus extremos. Esto es una fuente real de tensión. Los elementos anteriores se denominan fuentes ideales de tensión.
Una fuente real de corriente o tensión no es más que una fuente ideal que está acompañada de una resistencia en serie.
Rs no es más que la resistencia interna que tiene una batería, debido a todos los componentes que equipa. Esta Rs tendrá un valor mayor o menor, pero siempre estará, es decir, no existe ningún material en el universo con resistencia 0. Podría ser muy próxima a 0, pero no tendrá este valor exacto.
Para entender bien el funcionamiento de las baterías observemos el circuito de la izquierda. Está abierto, por lo que no puede haber intensidad de corriente. Como I=0, aplicando Ohm y 2da ley de Kirchoff tenemos que V=0*Rs+Vab. Puede llamar la atención que ponga Vab si no existe ningún elemento. Podemos pensar que lo que hay entre A y B es una resistencia de valor infinito (Si despejamos, (Vab/0)=Rab, y algo entre 0 es infinito) para entenderlo mejor. Por lo que en circuito abierto V=Vab. Es decir que si mido con un voltímetro los extremos de la pila marcará la tensión V de la fuente ideal. Por otra parte si conecto una resistencia R la cosa cambiaría (se trataría pues de un divisor de tensión, de manera que VR medida entre los puntos AB no sería igual que Vab hallada antes de la conexión). Si no ha quedado claro lo de Vab hay que tener en cuenta que en electricidad cuando hablamos de un punto eléctricamente igual que otro nos referimos a que tienen ambos la misma tensión. En este caso vemos que Va es distinto de Vb, no son el mismo punto, por lo tanto Vab=Va-Vb ya tiene un valor determinado que NO es 0. También se puede ver como que si no pasa corriente por Rs no puede haber ninguna caida de tensión en ella (es decir, que a efectos eléctricos es como si no existiera) de forma que solo consideraríamos la tensión de la fuente ideal.
Analizando todo lo anterior vemos que si Rs disminuye la caída de tensión en lo que vayamos a conectar sería más grande todavía. Pero si disminuye Rs al igual que una R conectada la intensidad sería muy grande.
Para el caso con fuente real de corriente se traduce en lo mismo que el divisor de corriente (Así que no veo necesaria su explicación si se ha entendido correctamente), donde la resistencia conectada a la batería es R´. Únicamente decir que lo único que cambiaría es la intensidad IR´ (cuyo valor sería fácil despejar de las ecuaciones previas).
Un cortocircuito se puede definir como la puesta de dos puntos al mismo potencial. Todo elemento que este entre ellos se dice que ha sido cortocircuitado. Sin embargo los efectos que puede generar este fenómeno son varios, dependerá pues de dicho elemento.
Por ejemplo, ¿que ocurre si cortocircuitamos una batería?
Imaginemos un circuito simple, donde tengo una fuente ideal de tensión y conecto con un cable de resistencia nula el polo positivo con el negativo. Si yo aplico la ley de Ohm al circuito para una tensión V dada, la intensidad I=V/0=Infinito, puesto que no hay resistencia alguna que se oponga al paso de corriente. No obstante en la realidad producir un cortocircuito de corriente infinita es impensable, pues como dije anteriormente no existe material con resistencia nula. De manera que si, la intensidad puede ser enorme, pero no infinita. Si en la vida real hacemos este experimento (equivaldría a cortocircuitar los puntos A y B de la fuente real de tensión) la pila se sobrecalentará, y eso hará que se descargue más rápido.
La razón de esto es el concepto de potencia o pérdidas por efecto Joule. En un cable de resistencia cualquiera R sufre un calentamiento producido por el paso de corriente I.
A la derecha se observa la fórmula fundamental. La potencia se puede definir como la energía en un determinado instante de tiempo. De manera que P=E/t=I^2*R. Analizándola se aprecia que la intensidad está al cuadrado, mientras que la resistencia no. Esto es importante, pues el verdadero culpable del calentamiento no es tanto R sino la corriente.
De hecho, en electricidad la corriente es la responsable de la mayoría de sucesos. Para que una corriente eléctrica sea peligrosa no es tan importante la tensión a la que esté un cable por ejemplo, lo es el valor de I. Es algo muy común asociar la alta tensión con riesgo eléctrico, pero no siempre es así (en la carrocería de los coches puede acumularse cientos de miles de voltios. Si alguna vez habéis tocado el mango de la puerta y os saltó una chispa pensad que os comisteis probablemente muchos mas voltios de los que tienes en el enchufe de vuestra casa). También es la responsable de la creación del campo magnético, la inducción y otros fenómenos electromagnéticos (plasmado en la 4ta ley de Maxwell, la cual ya comentaré).
Ahora pensemos que ocurriría si cortocircuitáramos una resistencia.
En este caso no hay mucho misterio. Para hacerlo conectemos el extremo de una con el final de la otra:
En el circuito de la izquierda R1 y R2 están cortocircuitadas, hemos usado el cable de la parte derecha del 1er dibujo para hacerlo. Como se ve, los extremos de las dos resistencias son eléctricamente idénticos, de manera que están a la misma tensión. Si aplico la Ley de Ohm en R1 vemos que V1-V1=0=I1*R1, con lo que I1=0. No pasa corriente ni por R1 ni por R2, ya que toda la intensidad se ha desviado por el cable sin resistencia. Esto es lógico puesto que en base a esta ley cuanta menos resistencia tenga un cable la intensidad será mayor (suponiendo la tensión constante).
TEOREMA DE MÁXIMA TRANSFERENCIA DE POTENCIA
Como ya hemos visto, un elemento del circuito consume o da potencia en función de si cae o genera tensión respectivamente. Para ello debemos de saber la dirección y sentido de todas las intensidades que afectan a dichos elementos.
Para definir este teorema adecuadamente supongamos una fuente real de tensión en la cual se conecta una resistencia de valor R (en los extremos A y B). Calculemos ahora la potencia consumida por dicha R:
Potencia generada por la fuente:
P (generada)=U*I
Potencias consumidas por R y Rs:
P (Rs)=I^2*Rs
P (R)=I^2*R
P (generada)=P (consumida)=I^2*Rs+I^2*R=I^2*(R+Rs)=U*I --> (despejando I) I=U/(R+Rs)
P (R)=(U^2/(R+Rs)^2)*R
Entonces para que esa resistencia que conectamos consuma la máxima potencia POSIBLE los valores de R y Rs tienen que ser el mismo.
Por lo que la ecuación nos queda:
P (R)=(U^2/(4*R^2))*R --> P (R)= (U^2)/(4*R)
Por ejemplo, si mi Rs= 1 ohmio, para transferir la potencia más grande que puede darle la fuente de tensión el valor de R= 1 ohmio.
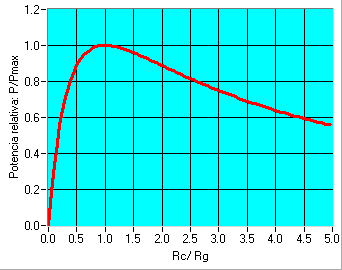
Diagrama de la máxima potencia transmitida (en el pico de la función es donde se alcanza la potencia más grande)
Se puede llegar a pensar que, para aumentar la potencia consumida por R habría simplemente que elevar el valor de esta, ya que si P=I^2*R, aumenta R, aumenta P. Es por esta razón que el teorema es trascendental e importante. Solo existe un valor de R para que se se transmita la máxima potencia, no por más que se incremente aumentará P.
NOTA: Los cálculos hechos anteriormente para este teorema son válidos para aplicarlos en cualquier momento donde se requiera saber por ejemplo cuanta potencia consume una resistencia de valor X ohmios.
Y hasta aquí la corriente continua. Espero que les haya gustado, si creéis que existe cualquier error ya bien sea por cálculo o explicación no dudéis en comentarlo.
Como artículo interesante te invito a leer acerca de los campos eólicos marítimos más grandes del mundo, tecnología muy interesante en el campo de energías renovables.
Toda esta información ha sido obtenida como estudiante de la Universidad Carlos III de Madrid.








Comentarios
Publicar un comentario